Access RBSE Solutions for Class 6 Chapter 10: Mensuration Navigating through the mathematical landscape of RBSE Class 6, the chapter on Mensuration (Chapter 10) holds significant importance. Understanding Mensuration is crucial as it not only enhances problem-solving skills but also plays a pivotal role in scoring well in annual exams. This article delves into the significance of RBSE Solutions for Class 6 Maths Chapter 10: Mensuration and how these solutions can be a game-changer for students aiming to excel in this subject.
Table of Contents

1. Unraveling the Importance of Chapter 10 – Mensuration:
Mensuration is a fundamental topic in mathematics, focusing on the measurement of geometric shapes and their parameters such as area and perimeter. In RBSE Class 6, mastering Mensuration is essential as it forms the basis for more advanced concepts in subsequent classes. This chapter is known for its prominence in annual exams, making it imperative for students to grasp its principles thoroughly.
2. Key Concepts in RBSE Class 6 Maths Chapter 10: Mensuration:
- Measurement of area and perimeter.
- Understanding basic geometric shapes.
- Applying Mensuration concepts to solve real-life problems.
- Practical examples to reinforce learning.
3. RBSE Solutions: Your Comprehensive Guide to Success:
Our RBSE Class 6 Maths Chapter 10: Mensuration solutions serve as a comprehensive guide for students, offering:
- Detailed explanations for each concept.
- Step-by-step solutions for problem-solving.
- Real-life applications to illustrate the relevance of Mensuration.
- Practice exercises to reinforce understanding.
4. Scoring High in Mathematics: A Strategic Approach:
- Conceptual Clarity: Our solutions focus on providing clear explanations, ensuring students comprehend the intricacies of Mensuration.
- Problem-Solving Mastery: A step-by-step approach to problem-solving empowers students to tackle complex questions with ease.
- Accessible Learning: Whether online or offline, our RBSE solutions are accessible at any time, offering flexibility in study routines.
RBSE Solutions for Class 6 Chapter 10 Exercise 10.1 Page No. 212
1. Find the perimeter of each of the following figures:
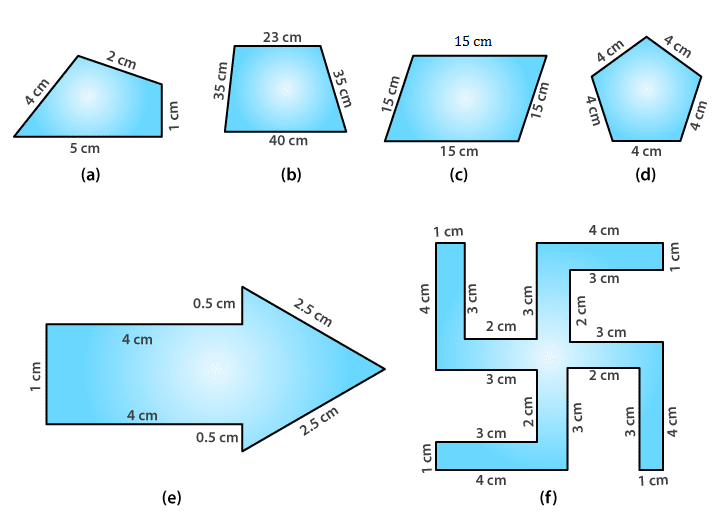
Solutions:
(a) Perimeter = Sum of all the sides
= 1 + 2 + 4 + 5
= 12 cm
(b) Perimeter = Sum of all the sides
= 23 + 35 + 35 + 40
= 133 cm
(c) Perimeter = Sum of all the sides
= 15 + 15 + 15 + 15
= 60 cm
(d) Perimeter = Sum of all the sides
= 4 + 4 + 4 + 4 + 4
=20 cm
(e) Perimeter = Sum of all the sides
= 1 + 4 + 0.5 + 2.5 + 2.5 + 0.5 + 4
= 15 cm
(f) Perimeter = Sum of all the sides
= 4 + 1 + 3 + 2 + 3 + 4 + 1 + 3 + 2 + 3 + 4 + 1 + 3 + 2 + 3 + 4 + 1 + 3 + 2 + 3
= 52 cm
2. The lid of a rectangular box, with sides 40 cm by 10 cm, is sealed all around with tape. What is the length of the tape required?
Solutions:
Length of required tape = Perimeter of rectangle
= 2 (Length + Breadth)
= 2 (40 + 10)
= 2 (50)
= 100 cm
∴ The required length of tape is 100 cm.
3. A table top measures 2 m 25 cm by 1 m 50 cm. What is the perimeter of the tabletop?
Solutions:
Length of tabletop = 2 m 25 cm = 2.25 m
Breadth of tabletop = 1 m 50 cm = 1.50 m
Perimeter of tabletop = 2 (Length + Breadth)
= 2 (2.25 + 1.50)
= 2 (3.75)
= 2 × 3.75
= 7.5 m
∴ The perimeter of the table top is 7.5 m.
4. What is the length of the wooden strip required to frame a photograph of length and breadth, 32 cm and 21 cm, respectively?
Solutions:
The required length of the wooden strip = Perimeter of the photograph
= 2 (Length + Breadth)
= 2 (32 + 21)
= 2 (53)
= 2 × 53
= 106 cm
∴ The required length of the wooden strip is 106 cm.
5. A rectangular piece of land measures 0.7 km by 0.5 km. Each side is to be fenced with 4 rows of wires. What is the length of the wire needed?
Solutions:
Perimeter of the field = 2 (Length + Breadth)
= 2 (0.7 + 0.5)
= 2 (1.2)
= 2 × 1.2
= 2.4 km
Each side is to be fenced with 4 rows = 4 × 2.4
= 9.6 km
∴ The total length of the required wire is 9.6 km.
6. Find the perimeter of each of the following shapes:
(a) A triangle of sides 3 cm, 4 cm and 5 cm
(b) An equilateral triangle of side 9 cm
(c) An isosceles triangle with equal sides of 8 cm each and the third side of 6 cm.
Solutions:
(a) Perimeter of triangle = 3 + 4 + 5
= 12 cm
(b) Perimeter of an equilateral triangle = 3 × side
= 3 × 9
= 27 cm
(c) Perimeter of isosceles triangle = 8 + 8 + 6
= 22 cm
7. Find the perimeter of a triangle with sides measuring 10 cm, 14 cm and 15 cm.
Solutions:
Perimeter of triangle = 10 + 14 + 15
= 39 cm
∴ The perimeter of the triangle is 39 cm.
8. Find the perimeter of a regular hexagon with each side measuring 8 m.
Solutions:
Perimeter of hexagon = 6 × 8
= 48 m
∴ The perimeter of the regular hexagon is 48 m.
9. Find the side of the square whose perimeter is 20 m.
Solutions:
Perimeter of square = 4 × side
20 = 4 × side
Side = 20 / 4
Side = 5 m
∴ The side of the square is 5 m.
10. The perimeter of a regular pentagon is 100 cm. How long is its each side?
Solutions:
The perimeter of the regular pentagon = 100 cm
5 × side = 100 cm
Side = 100 / 5
Side = 20 cm
∴ The side of the pentagon is 20 cm.
11. A piece of string is 30 cm long. What will be the length of each side if the string is used to form:
(a) a square?
(b) an equilateral triangle?
(c) a regular hexagon?
Solutions:
(a) Perimeter of square = 30 cm
4 × side = 30
Side = 30 / 4
Side = 7.5 cm
(b) Perimeter of equilateral triangle = 30 cm
3 × side = 30
Side = 30 / 3
Side = 10 cm
(c) Perimeter of regular hexagon = 30 cm
6 × side = 30
Side = 30 / 6
Side = 5 cm
12. Two sides of a triangle are 12 cm and 14 cm. The perimeter of the triangle is 36 cm. What is its third side?
Solutions:
Let x cm be the third side
Perimeter of triangle = 36 cm
12 + 14 + x = 36
26 + x = 36
x = 36 – 26
x = 10 cm
∴ The third side is 10 cm.
13. Find the cost of fencing a square park of side 250 m at the rate of ₹ 20 per metre.
Solutions:
Side of square = 250 m
Perimeter of square = 4 × side
= 4 × 250
= 1000 m
Cost of fencing = ₹ 20 per m
Cost of fencing for 1000 m = ₹ 20 × 1000
= ₹ 20,000
∴ The cost of fencing the square park is ₹ 20,000.
14. Find the cost of fencing a rectangular park of length 175 cm and breadth 125 m at the rate of ₹ 12 per metre.
Solutions:
Length = 175 cm
Breadth = 125 m
Perimeter of rectangular park = 2 (Length + Breadth)
= 2 (175 + 125)
= 2 (300)
= 2 × 300
= 600 m
Cost of fencing = 12 × 600
= 7200
∴ The cost of fencing is ₹ 7,200.
15. Sweety runs around a square park of side 75 m. Bulbul runs around a rectangular park with a length of 60 m and a breadth of 45 m. Who covers less distance?
Solutions:
Perimeter of square = 4 × side
= 4 × 75
= 300 m
∴ The distance covered by Sweety is 300 m
Perimeter of the rectangular park = 2 (Length + Breadth)
= 2 (60 + 45)
= 2 (105)
= 2 × 105
= 210 m
∴ The distance covered by Bulbul is 210 m
Hence, Bulbul covers less distance than Sweety.
16. What is the perimeter of each of the following figures? What do you infer from the answers?
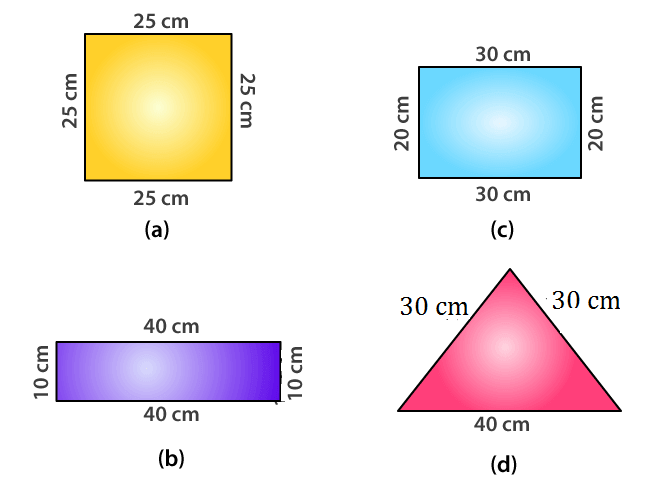
Solutions:
(a) Perimeter of square = 4 × side
= 4 × 25
= 100 cm
(b) Perimeter of rectangle = 2 (40 + 10)
= 2 × 50
= 100 cm
(c) Perimeter of rectangle = 2 (Length + Breadth)
= 2 (30 + 20)
= 2 (50)
= 2 × 50
= 100 cm
(d) Perimeter of triangle = 30 + 30 + 40
= 100 cm
∴ All the figures have the same perimeter.
17. Avneet buys 9 square paving slabs, each with a side of 1 / 2 m. He lays them in the form of a square.
(a) What is the perimeter of his arrangement [fig 10.7(i)]?

(b) Shari does not like his arrangement. She gets him to lay them out like a cross. What is the perimeter of her arrangement [(Fig 10.7 (ii)]?
(c) Which has a greater perimeter?
(d) Avneet wonders if there is a way of getting an even greater perimeter. Can you find a way of doing this? (The paving slabs must meet along complete edges, i.e. they cannot be broken.)
Solutions:
(a) Side of square = 3 × side
= 3 × 1 / 2
= 3 / 2 m
Perimeter of Square = 4 × 3 / 2
= 2 × 3
= 6 m
(b) Perimeter = 0.5 + 1 + 1 + 0.5 + 1 + 1 + 0.5 + 1 + 1 + 0.5 + 1 + 1
= 10 m
(c) The arrangement in the form of a cross has a greater perimeter.
(d) Perimeters greater than 10 m cannot be determined.
RBSE Solutions for Class 6 Chapter 10 Exercise 10.2 Page No. 216
1. Find the areas of the following figures by counting squares:


(a) The figure contains only 9 fully filled squares. Hence, the area of this figure will be 9 square units.
(b) The figure contains only 5 fully filled squares. Hence, the area of this figure will be 5 square units.
(c) The figure contains 2 fully filled squares and 4 half filled squares. Hence, the area of this figure will be 4 square units.
(d) The figure contains only 8 fully filled squares. Hence, the area of this figure will be 8 square units.
(e) The figure contains only 10 fully filled squares. Hence, the area of this figure will be 10 square units.
(f) The figure contains only 2 fully filled squares and 4 half filled squares. Hence, the area of this figure will be 4 square units.
(g) The figure contains 4 fully filled squares and 4 half filled squares. Hence, the area of this figure will be 6 square units.
(h) The figure contains 5 fully filled squares. Hence, the area of this figure will be 5 square units.
(i) The figure contains 9 fully filled squares. Hence, the area of this figure will be 9 square units.
(j) The figure contains 2 fully filled squares and 4 half filled squares. Hence, the area of this figure will be 4 square units.
(k) The figure contains 4 fully filled squares and 2 half filled squares. Hence, the area of this figure will be 5 square units.
(l) From the given figure, we observe
| Covered Area | Number | Area Estimate (square units) |
| Fully filled squares | 2 | 2 |
| Half filled squares | – | – |
| More than half filled squares | 6 | 6 |
| Less than half filled squares | 6 | 0 |
Therefore total area = 2 + 6
= 8 square units.
(m) From the given figure, we observe
| Covered Area | Number | Area Estimate (square units) |
| Fully filled squares | 5 | 5 |
| Half filled squares | – | – |
| More than half filled squares | 9 | 9 |
| Less than half filled squares | 12 | 0 |
Therefore total area = 5 + 9
= 14 square units
(n) From the given figure, we observe
| Covered Area | Number | Area estimate (square units) |
| Fully filled squares | 8 | 8 |
| Half filled squares | – | – |
| More than half filled squares | 10 | 10 |
| Less than half filled squares | 9 | 0 |
Therefore total area = 8 + 10 = 18 square units
RBSE Solutions for Class 6 Chapter 10 Exercise 10.3 Page No. 219
1. Find the area of the rectangles whose sides are:
(a) 3 cm and 4 cm
(b) 12 m and 21 m
(c) 2 km and 3 km
(d) 2 m and 70 cm
Solutions:
We know that
Area of rectangle = Length × Breadth
(a) l = 3 cm and b = 4 cm
Area = l × b = 3 × 4
= 12 cm2
(b) l = 12 m and b = 21 m
Area = l × b = 12 × 21
= 252 m2
(c) l = 2 km and b = 3 km
Area = l × b = 2 × 3
= 6 km2
(d) l = 2 m and b = 70 cm = 0.70 m
Area = l × b = 2 × 0.70
= 1.40 m2
2. Find the areas of the squares whose sides are:
(a) 10 cm
(b) 14 cm
(c) 5 m
Solutions:
(a) Area of square = side2
= 102
= 100 cm2
(b) Area of square = side2
= 142
= 196 cm2
(c) Area of square = side2
= 52
=25 cm2
3. The length and breadth of the three rectangles are as given below:
(a) 9 m and 6 m
(b) 17 m and 3 m
(c) 4 m and 14 m
Which one has the largest area, and which one has the smallest?
Solutions:
(a) Area of rectangle = l × b
= 9 × 6
= 54 m2
(b) Area of rectangle = l × b
= 17 × 3
= 51 m2
(c) Area of rectangle = l × b
= 4 × 14
= 56 m2
The area of rectangle 56 m2, i.e. (c), is the largest area and the area of rectangle 51 m2, i.e. (b), is the smallest area
4. The area of a rectangular garden 50 m long is 300 sq m. Find the width of the garden.
Solutions:
Area of rectangle = length × width
300 = 50 × width
width = 300 / 50
width = 6 m
∴ The width of the garden is 6 m.
5. What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of ₹ 8 per hundred sq m?
Solutions:
Area of land = length × breadth
= 500 × 200
= 1,00,000 m2
∴ Cost of tiling 1,00,000 sq m of land = (8 × 1,00,000) / 100
= ₹ 8000
∴ The cost of tiling a rectangular plot of land is ₹ 8000.
6. A tabletop measures 2 m by 1 m 50 cm. What is its area in square metres?
Solutions:
Given
l = 2m
b = 1m 50 cm = 1.50 m
Area = l × b = 2 × 1.50
= 3 m2
∴ The area of the tabletop is 3 m2.
7. A room is 4 m long and 3 m 50 cm wide. How many square metres of carpet are needed to cover the floor of the room?
Solutions:
Given
l = 4m
b = 3 m 50 cm = 3.50 m
Area = l × b = 4 × 3.50
= 14 m2
∴ The carpet required to cover the floor is 14 m2.
8. A floor is 5 m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.
Solutions:
Area of floor = l × b = 5 × 4
= 20 m2
Area of square carpet = 3 × 3
= 9 m2
Area of floor that is not carpeted = 20 – 9
= 11 m2
∴ The area of the floor that is not carpeted is 11 m2.
9. Five square flower beds, each of sides 1 m, are dug on a piece of land 5 m long and 4 m wide. What is the area of the remaining part of the land?
Solutions:
Area of flower square bed = 1 × 1
= 1 m2
Area of 5 square bed = 1 × 5
= 5 m2
Area of land = 5 × 4
= 20 m2
Remaining part of the land = Area of land – Area of 5 square bed
= 20 – 5
= 15 m2
∴ The remaining part of the land is 15 m2.
10. By splitting the following figures into rectangles, find their areas (The measures are given in centimetres).
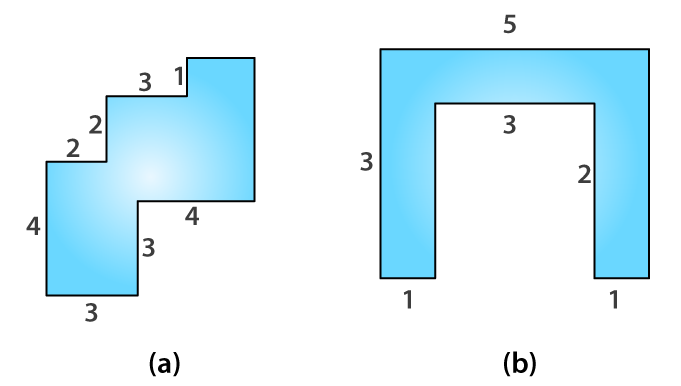
Solutions:
(a)
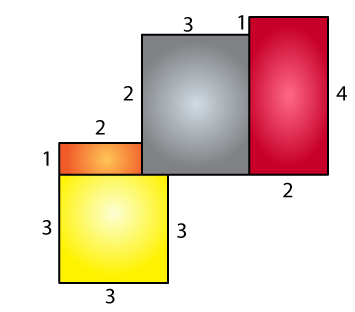
Area of yellow region = 3 × 3
= 9 cm2
Area of orange region = 1× 2
= 2 cm2
Area of grey region = 3 × 3
= 9 cm2
Area of brown region = 2 × 4
= 8 cm2
Total area = 9 + 2 + 9 + 8
= 28 cm2
∴ The total area is 28 cm2.
(b)
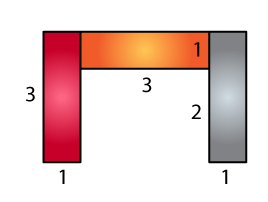
Area of brown region = 3 × 1
= 3 cm2
Area of orange region = 3 × 1
= 3 cm2
Area of grey region = 3 × 1
= 3 cm2
Total area = 3 + 3 + 3
= 9 cm2
∴ The total area is 9 cm2.
11. Split the following shapes into rectangles and find their areas. (The measures are given in centimetres)
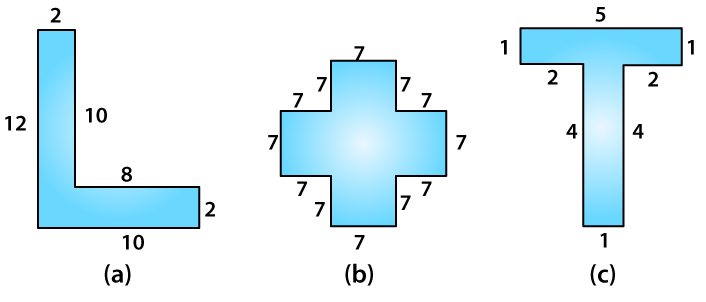
Solutions:
(a)
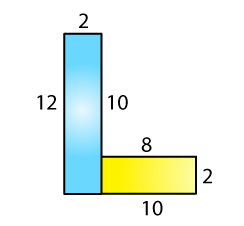
Total area of the figure = 12 × 2 + 8 × 2
= 40 cm2
(b)
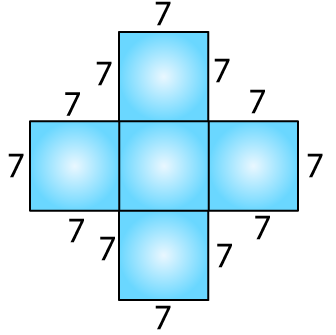
There are 5 squares, and each side is 7 cm.
Area of 5 squares = 5 × 72
= 245 cm2
(c)

Area of grey rectangle = 2 × 1
= 2 cm2
Area of brown rectangle = 2 × 1
= 2 cm2
Area of orange rectangle = 5 × 1
= 5 cm2
Total area = 2 + 2 + 5
= 9 cm2
12. How many tiles whose length and breadth are 12 cm and 5 cm, respectively, will be needed to fit in a rectangular region whose length and breadth are respectively:
(a) 100 cm and 144 cm?
(b) 70 cm and 36 cm?
Solutions:
(a) Area of rectangle = 100 × 144
= 14400 cm
Area of one tile = 5 × 12
= 60 cm2
Number of tiles = (Area of rectangle) / (Area of one tile)
= 14400 / 60
= 240
Hence, 240 tiles are needed
(b) Area of rectangle = 70 × 36
= 2520 cm2
Area of one tile = 5 × 12
= 60 cm2
Number of tiles = (Area of rectangle) / (Area of one tile)
= 2520 / 60
= 42
Hence, 42 tiles are needed.
In the pursuit of academic excellence, RBSE Class 6 students can significantly benefit from our SEO-friendly article highlighting the importance of mastering Mensuration. With RBSE Solutions for Class 6 Maths Chapter 10, students gain access to a wealth of knowledge and a strategic approach to problem-solving. Scoring high marks in mathematics becomes achievable with a solid understanding of Mensuration, setting the stage for future mathematical success.
